三大相关系数
# 1、三大相关系数
## 1.1 Pearson相关系数
要理解Pearson相关系数,首先要理解协方差(Covariance),协方差是一个反映两个随机变量相关程度的指标,如果一个变量跟随着另一个变量同时变大或者变小,那么这两个变量的协方差就是正值,反之相反,公式如下:
::: hljs-center
$cov(X, Y)=\frac{\sum_{n}^{i=1}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{n-1}$
:::
Pearson相关系数公式如下:
::: hljs-center
$\rho_{X, Y}={corr}(X, Y)=\frac{{cov}(X, Y)}{\sigma_{X} \sigma_{Y}}=\frac{E\left[\left(X-\mu_{X}\right)\left(Y-\mu_{Y}\right)\right]}{\sigma_{X} \sigma_{Y}}$
:::
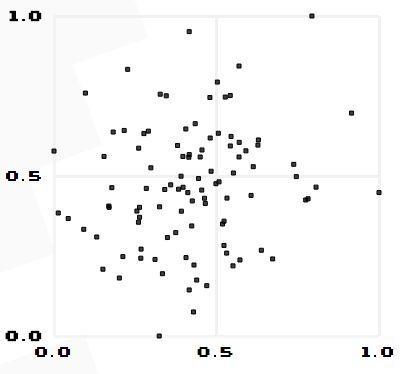
由公式可知,Pearson相关系数是用协方差除以两个变量的标准差得到的,虽然协方差能反映两个随机变量的相关程度(协方差大于0的时候表示两者正相关,小于0的时候表示两者负相关),但是协方差值的大小并不能很好地度量两个随机变量的关联程度,例如,现在二维空间中分布着一些数据,我们想知道数据点坐标X轴和Y轴的相关程度,如果X与Y的相关程度较小但是数据分布的比较离散,这样会导致求出的协方差值较大,用这个值来度量相关程度是不合理的,如下图:
::: hljs-center
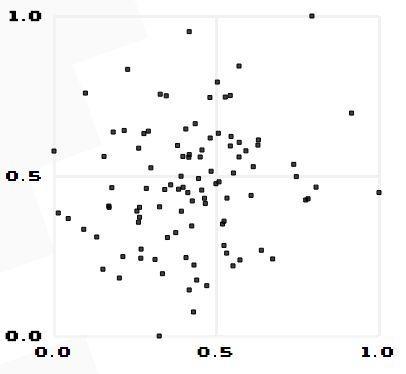
:::
为了更好的度量两个随机变量的相关程度,引入了Pearson相关系数,其在协方差的基础上除以了两个随机变量的标准差,容易得出,pearson是一个介于-1和1之间的值,当两个变量的线性关系增强时,相关系数趋于1或-1;当一个变量增大,另一个变量也增大时,表明它们之间是正相关的,相关系数大于0;如果一个变量增大,另一个变量却减小,表明它们之间是负相关的,相关系数小于0;如果相关系数等于0,表明它们之间不存在线性相关关系。《数据挖掘导论》给出了一个很好的图来说明:
::: hljs-center
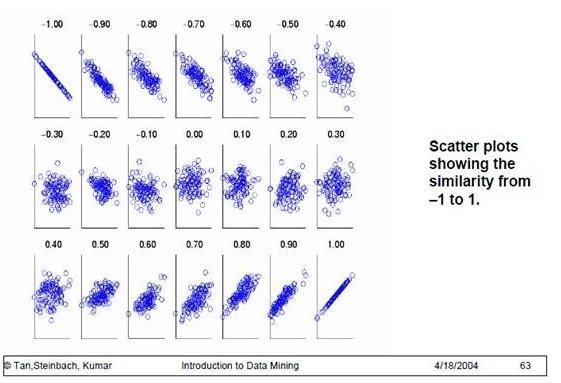
:::
从泛函分析的角度看,相关系数就是两个n维随机向量夹角的余弦值,取值都为-1~1,越接近1,向量夹角越小,两个向量的正相关性就越大。相关系数的公式其实也是向量夹角的余弦公式:cos(a,b)=a·b/(|a|*|b|)
>当两个变量的标准差都不为零时,相关系数才有定义
>**皮尔逊相关系数适用于:**
>1. 两个变量之间是线性关系,都是连续数据。
>2. 两个变量的**总体**是正态分布,或接近正态的单峰分布。[双变量正态分布的检验](https://zhuanlan.zhihu.com/p/343723744?ivk_sa=1024320u)
>3. 两个变量的观测值是成对的,每对观测值之间相互独立。
>4. 应该没有异常值 (受异常值影响大)
为啥通常会假设为正态分布呢?因为我们在求皮尔森相关性系数以后,通常还会用t检验之类的方法来进行皮尔森相关性系数检验,而 t检验是基于数据呈正态分布的假设的。
转载:[如何理解皮尔逊相关系数(Pearson Correlation Coefficient)? - TimXP的回答 - 知乎](https://www.zhihu.com/question/19734616/answer/117730676)
-----
## 1.2 Spearman相关系数
Spearman秩相关系数是一个非参数性质(与分布无关)的秩统计参数,通常被认为是排列后的变量之间的Pearson线性相关系数,在实际计算中,有更简单的计算$\rho_{s}$的方法。假设原始的数据$x_{i}$, $y_{i}$已经按从大到小的顺序排列,记$R\left(x_{i}\right)$是$x_{i}$在$x$中的大小排名名次,$R\left(y_{i}\right)$是$y_{i}$在$y$中的大小排名名次,$\overline{R(x)}$是x名次均值,$\overline{R(y)}$是y名次均值,n为数据对个数。则Spearman秩相关系数为:
::: hljs-center
$\rho=\frac{\sum_{i=1}^{n}\left(R\left(x_{i}\right)-\overline{R(x)}\right)\left(R\left(y_{i}\right)-\overline{R(y)}\right)}{\sqrt{\sum_{i=1}^{n}\left(R\left(x_{i}\right)-\overline{R(x)}\right)^{2} \cdot \sum_{i=1}^{n}\left(R\left(y_{i}\right)-\overline{R(y)}\right)^{2}}}=1-\frac{6 \sum_{i=1}^{n}\left(R\left(x_{i}\right)-R\left(y_{i}\right)\right)^{2}}{n\left(n^{2}-1\right)}$
:::
>**斯皮尔曼相关系数适用于:**
斯皮尔曼等级相关系数对数据条件的要求没有皮尔逊相关系数严格
**只要两个变量的观测值是成对的等级评定资料**,或者是**由连续变量观测资料转化得到的等级资料**,不论两个变量的总体分布形态、样本容量的大小如何,都可以用斯皮尔曼等级相关系数来进行研究。
----
## 1.3 Kendall相关系数
假设两个随机变量分别为$x,y$(也可以看做两个集合),它们的元素个数均为N,两个随机变量取的第 i(1<=i<=N)个值分别用$x_{i}$、$y_{i}$表示。x与y中的对应元素组成一个元素对集合$xy$,其包含的元素为($x_{i}$, $y_{i}$)(1<=i<=N)。当集合xy中任意两个元素($x_{i}$, $y_{i}$)与($x_{j}$, $y_{j}$)的排行相同时(也就是说当出现情况1或2时;情况1:$x_{i}$>$x_{j}$且$y_{i}$>$y_{j}$,情况2:$x_{i}$<$x_{j}$且$y_{i}$<$y_{j}$),这两个元素就被认为是一致的。当出现情况3或4时(情况3:$x_{i}$>$x_{j}$且$y_{i}$<$y_{j}$,情况4:$x_{i}$<$x_{j}$且$y_{i}$>$y_{j}$),这两个元素被认为是不一致的。当出现情况5或6时(情况5:$x_{i}$=$x_{j}$,情况6:$y_{i}$=$y_{j}$),这两个元素既不是一致的也不是不一致的。
**公式一:**
$T a u-a=\frac{C-D}{\frac{1}{2} N(N-1)}$
其中C表示xy中拥有一致性的元素对数(两个元素为一对);D表示XY中拥有不一致性的元素对数。
注意:这一公式仅适用于集合x与y中均不存在相同元素的情况(集合中各个元素唯一)。
**公式二:**
$T a u-b=\frac{C-D}{\sqrt{(N 3-N 1)(N 3-N 2)}}$
注意:这一公式适用于集合x或y中存在相同元素的情况(当然,如果x或y中均不存在相同的元素时,公式二便等同于公式一)。
其中C、D与公式一中相同;
$N 3=\frac{1}{2} N(N-1) \quad N 1=\sum_{i=1}^{s} \frac{1}{2} U_{i}\left(U_{i}-1\right) \quad N 2=\sum_{i=1}^{t} \frac{1}{2} V_{i}\left(V_{i}-1\right)$
N1、N2分别是针对集合x、y计算的,现在以计算N1为例,给出N1的由来(N2的计算可以类推):
将x中的相同元素分别组合成小集合,s表示集合x中拥有的小集合数(例如x包含元素:1 2 3 4 3 3 2,那么这里得到的s则为2,因为只有2、3有相同元素),Ui表示第i个小集合所包含的元素数。N2在集合y的基础上计算而得。
**公式三:**
$T a u-c=\frac{C-D}{\frac{1}{2} N^{2} \frac{M-1}{M}}$
注意:这一公式中没有再考虑集合X、或Y中存在相同元素给最后的统计值带来的影响。公式三的这一计算形式仅适用于用表格表示的随机变量X、Y之间相关系数的计算(下面将会介绍)。
>**肯德尔相关系数适用于:**
>肯德尔相关系数与斯皮尔曼相关系数对数据条件的要求相同,可参见[统计相关系数(2)--Spearman Rank(斯皮尔曼等级)相关系数及MATLAB实现](http://blog.csdn.net/wsywl/archive/2010/09/02/5859751.aspx)中介绍的斯皮尔曼相关系数对数据条件的要求。
参考:[https://blog.csdn.net/u011089523/article/details/53056829](https://blog.csdn.net/u011089523/article/details/53056829)
-----
# 2、每种相关性的比较
## 2.1 Pearson相关与Spearman和Kendall相关
非参数相关(指 spearman和hendall)的表达能力相对较弱,因为它们在计算中使用的信息较少。在Pearson的情况下,相关性使用有关均值和均值偏差的信息,而非参数相关性仅使用序数信息和成对分数。
在非参数相关的情况下,X和Y值可能是连续的或有序的,并且不需要X和Y的近似正态分布。但在皮尔逊相关的情况下,它假定X和Y的分布应该是正态分布,并且也应该是连续的(因此做spearman之前要做一些对数变换之类的尽量接近正态分布)。
## 2.2 Spearman相关与Kendall相关
在正常情况下,Kendall相关性比Spearman相关性更强健和有效。这意味着当样本量较小或存在一些异常值时,首选Kendall相关。
相关系数是测量**线性**(皮尔逊)或 **单调**(Spearman和Kendall)关系。
----
# 3、实战效果
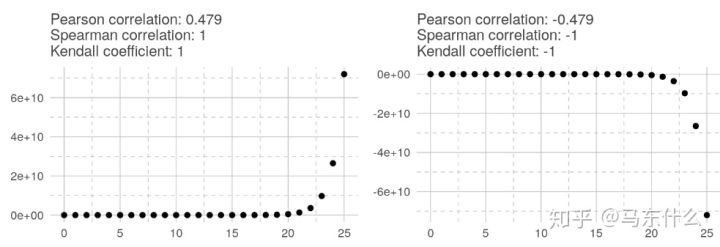
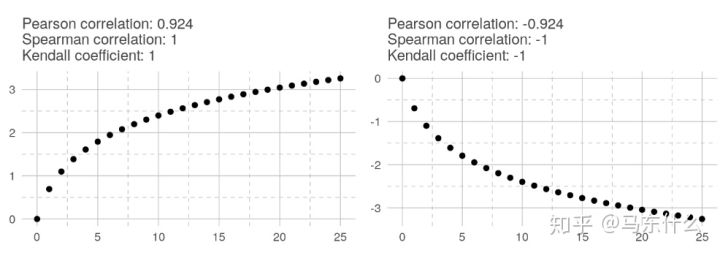
在线性关系中,所有相关系数均为1。
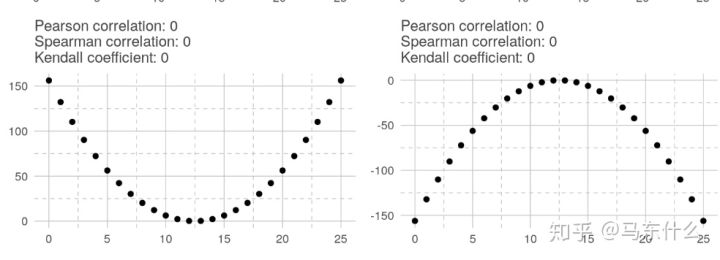
在指数关系中,只有两个非参数相关系数为1或-1。 在对数关系中,结果与指数关系相同。
在对称的U形关系中,所有相关系数均为零
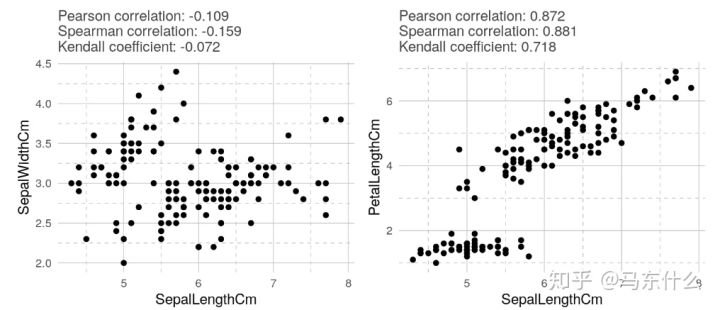
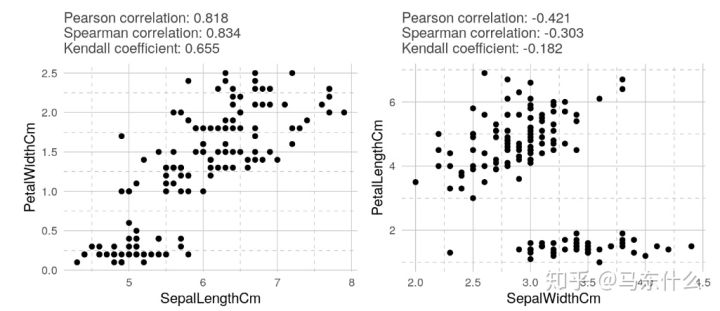
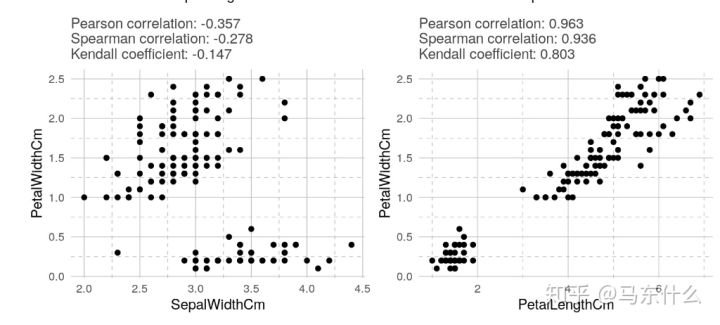
在所有情况下,Kendall相关系数的绝对值均小于其他绝对值。 可以看出,肯德尔相关性比其他相关性更为保守。