决策树-分类
**核心:特征选择+剪枝**
## 1 概述
决策树采取了“分而治之”的思想,是一种基本的分类方法,也可以用于回归。包括3个步骤:特征选择、决策树的生成和决策树的修剪。主要有ID3、C4.5和CART三种算法。
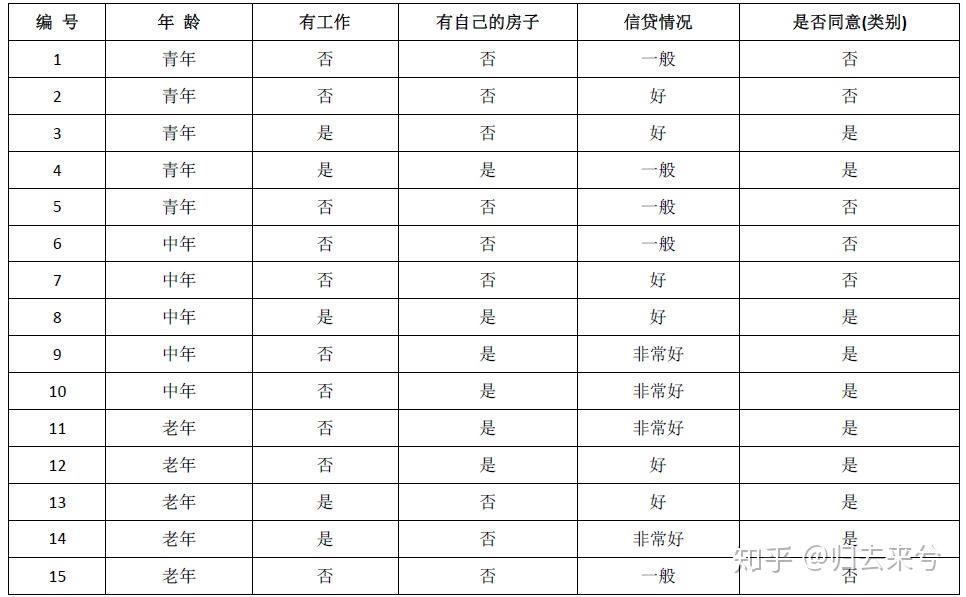
从形式上,决策树就是一棵按照各个特征建立的树形结构,叶节点表示对于的类别,特征选择的顺序不同,得到的树的形状也不同。我们追求的是模型简单、效果好,直观上也就是建立的决策树深度越小越好。
::: hljs-center
:::
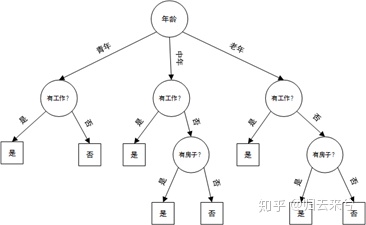
可以这样做:先看年龄(根节点),再看工作-房子-信贷,得到的决策树为
::: hljs-center
:::
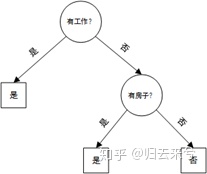
也可以这样做:按照工作-房子-年龄-信贷的顺序来看,得到的决策树如下
::: hljs-center
:::
可以看到,选择不同的特征顺序会得到不同的树形结构,显然第二种方法得到的决策树更简单,分类效率更高。那么到底该怎样选择特征更好呢?直观上,如果一个特征在当前条件下具有最好的分类能力,那么就应该选择这个特征。这一准则如何定量描述呢?
有三种方式:**信息增益、信息增益率、基尼指数**,
**分别对应**的决策树分类算法为**ID3、C4.5、CART**(三者的不同之处就是特征选择准则,算法思路没有差异)。
## 2 划分特征选择
### 2.1 信息增益
特征A对训练数据集D的信息增益定义为D的信息熵与A条件下的条件熵之差,即
$g(D, A)=H(D)-H(D \mid A)$
其中
$H(D)=-\sum_{i=1}^{k} \frac{\left|D^{i}\right|}{|D|} \log \frac{\left|D^{i}\right|}{|D|}$
$k$为类别数 , $H(D\mid A)=\sum_{i=1}^{n} \frac{\left|D^{i}\right|}{|D|} H\left(D^{i}\right)$ , $n$为特征A的取值个数。
[信息熵参考](https://blog.csdn.net/Albert201605/article/details/81427658)
熵是随机变量不确定性的度量,根据上式,信息增益表示的是给定一个特征条件下,原数据集不确定度的缩减量,也就是特征A对数据集不确定性的消除程度,反映了其分类能力(其实也就是D与A的互信息,即数据集D中含有的特征A的信息量)。**信息增益准则偏向于选择取值较多的特征**(如上例中以编号作为选取特征,则g(D,编号)=H(D)有最大值)。
### 2.2 信息增益率
特征A对训练数据集D的信息增益率定义为其信息增益与数据集D关于特征A的取值的熵之比,即
$g_{R}(D, A)=\frac{g(D, A)}{H_{A}(D)}$
其中 $H_{A}(D)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \log \frac{\left|D_{i}\right|}{|D|}$ , $n$为特征$A$的取值个数
### 2.3 基尼指数
1. 分类问题中,假设有k个类,样本点属于第i类的概率为 [公式] ,则概率分布的基尼指数定义为
${Gini}(p)=\sum_{i=1}^{k} p_{i}\left(1-p_{i}\right)=1-\sum_{i=1}^{k} p_{i}^{2}$
对于二类分类问题,若样本点属于第1个类的概率是$p$,则概率分布的基尼指数为
${Gini}(p)=2 p(1-p)$
2. 对于给定的样本集合$D$,其基尼指数为
${Gini}(D)=1-\sum_{i=1}^{k}\left(\frac{\left|D_{i}\right|}{|D|}\right)^{2}$
其中,$D_{i}$是$D$中属于第$i$类的样本集合,$k$是类的个数。
3. 如果样本集合$D$根据特征A是否取某一可能值$a$被分割成$D_1$和$D_2$两部分,即 $D_{1}=\{(x, y) \in D \mid A(x)=a\}, D_{2}=D-D_{1}$,则在特征A的条件下,集合D的基尼指数定义为
${Gini}(D, A)=\frac{\left|D_{1}\right|}{|D|} {Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} {Gini}\left(D_{2}\right)$
基尼指数${Gini}(D)$表示集合$D$的不确定性,基尼指数$Gini(D,A)$ 表示经 $A=a$ 分割后集合$D$的不确定性。基尼指数越大,集合样本的不确定性也就越大,这点与熵相似。
**[例]**
以ID3算法对上例数据建立决策树,也就是以信息增益作为特征选择准则,做法如下:
1) **根节点选择:**
$H(D)=-\frac{9}{15} \log \frac{9}{15}-\frac{6}{15} \log \frac{6}{15}=0.971($bit$)$
$g\left(D, A_{1}\right)=H(D)-\left[\frac{5}{15} H\left(D_{1}\right)+\frac{5}{15} H\left(D_{2}\right) \frac{5}{15} H\left(D_{3}\right)\right]=0.083$
$g\left(D, A_{2}\right)=H(D)-\left[\frac{5}{15} H\left(D_{1}\right)+\frac{10}{15} H\left(D_{2}\right)\right]=0.324$
同理,$g\left(D, A_{3}\right)=0.420, \quad g\left(D, A_{4}\right)=0.363$
由于特征$A_{3}$的信息增益最大,所以选择$A_{3}$作为根节点,易知 $A_{3}$取“是”时(子集$D_{1}$)只有同一类样本点,为叶节点。
2) **接着对$A_{3}$取“否”时(子集$D_{2}$)计算信息增益,选择第二层节点:**
$g\left(D_{2}, A_{1}\right)=H\left(D_{2}\right)-H\left(D_{2} \mid A_{1}\right)=0.918-0.667=0.251$
$g\left(D_{2}, A_{2}\right)=H\left(D_{2}\right)-H\left(D_{2} \mid A_{2}\right)=0.918$
$g\left(D_{2}, A_{4}\right)=H\left(D_{2}\right)-H\left(D_{2} \mid A_{4}\right)=0.474$
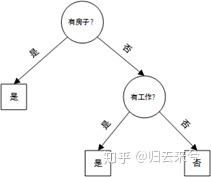
选择信息增益最大的特征$A_{2}$(有工作) 为特征节点,易知当$A_{2}$取“是”或“否”时,样本都属于同一类,所以就是两个叶节点。
这样,生成的一棵决策树为
::: hljs-center
:::
## 3 剪枝
上面的例子中只有树的生成,对训练数据有很精确的分类效果,但分支太多了就容易过拟合,所以需要进行剪枝(pruning)处理。剪枝策略有**预剪枝**和**后剪枝**。
**a. 预剪枝**
预剪枝是指在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点。
至于性能的判断有不同的评估方法,如采用留出法(预留一部分数据作验证集),就是每划分一个结点前都计算划分前划分后的验证集准确率,如果准确率提高了就划分,否则就不划分。
- 优点:降低了过拟合风险,减少了训练时间和测试时间开销。
- 缺点:**欠拟合**风险。
**b. 后剪枝**
后剪枝是先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点。
如性能评估采用留出法,就是对一棵已建立的决策树,自底向上对每棵子树进行判断:将该结点替换为叶结点(归为训练集中样本最多的类别),在验证集上的准确率是否提升?若提升则剪之;反之不剪。
后剪枝更一般化的评估方法是极小化决策树整体损失函数 $C_{\alpha}(T)=C(T)+\alpha|T|$ ,其中 $C(T)$ 表示模型对训练数据的预测误差, $|T|$ 表示模型复杂度,参数 $\alpha \geqslant 0$ 控制两者之间的影响。 $\alpha$ 较大偏向于使模型简化; $\alpha$ 较小则偏向于使训练集误差减小,即和训练集拟合程度高,模型越复杂(李航《统计学习方法》)。
- 优点:欠拟合风险小,泛化能力优于预剪枝。
- 缺点:训练时间开销大。
## 4 连续值与缺失值处理
### 4.1 连续值处理:二分法
前面的例子中各属性都是离散的,在一些其他问题中可能会出现连续的属性,即该特征取值为连续型随机变量,一种简单的处理方法是二分法。顾名思义,二分法就是在该连续属性中找一个点一分为二,大的一个分支,小的一个分支。
在训练集D中,假定连续属性a共有n个不同的取值,将这些值从小到大进行排序,记为 $\left\{a^{1}, a^{2}, \ldots, a^{n}\right\}$。 一个划分点t可将$D$分为两部分,一部分是不大于t的样本,记为 $D_{t}^{-}$ ;一部分是大于t的样本,记为 $D_{t}^{+}$ . 我们把每个小区间 $\left[a^{i}, a^{i+1}\right)$ 的中位点 $\frac{a^{i}+a^{i+1}}{2}$ 作为候选划分点,只要在这n-1个点中找到一个最优的即可,也就是要找到一个使得信息增益最大的划分点,需满足:
::: hljs-center
$g(D, a)=\max g(D, a, t)=\max \left[H(D)-\sum_{\lambda \in\{-,+\}} \frac{\left|D_{t}^{\lambda}\right|}{|D|} H\left(D_{t}^{\lambda}\right)\right]$
:::
其中 $g(D, a, t)$ 是训练集D基于划分点t二分后的信息增益,即 $t={artmax} g(D, a, t)$ .
需注意的是,与离散属性不同,若当前结点划分属性为连续属性,该属性仍可作为其后代结点的划分属性(如父结点使用“密度>0.381”,子结点也可能使用“密度>0.563”)。
### 4.2 缺失值处理
为有效利用现有的数据样本,需要对一些属性缺失的样本进行处理。显然对要建立的决策树,面临的两个问题是
1) 如何进行划分特征的选择?
2) 若属性缺失,如何对样本划分?
这里先对训练集中每个样本赋予一个权重 $w_x$ ,并全部初始化为1。
**a. 特征选择:信息增益加权**
既然有的样本属性缺失,那我们就按那些不缺失的计算出信息增益,再按样本比例赋上一个权重。可描述为:在训练集D中,D’为属性a上没有缺失值的样本子集,则该属性的信息增益为
::: hljs-center
$g(D, a)=\rho \times g\left(D^{\prime}, a\right),$ 其中 $\rho=\frac{\sum_{x \in D^{\prime}} w_{x}}{\sum_{x \in D} w_{x}}$
:::
**b. 样本划分:加权划分**
若样本$x$在该属性不缺失,则将其划入对应的子结点,且**样本权值**在子结点中保持为 $W_x$ 不变。若样本x在该属性缺失,则将其以权值 $\frac{\sum_{x \in D^{\prime} v} w_{x}}{\sum_{x \in D^{\prime}} w_{x}} \cdot w_{x}$ 同时划分到所有子结点。其中比值 $\frac{\sum_{x \in D^{\prime} v} w_{x}}{\sum_{x \in D^{\prime}} w_{x}}$ 表示无缺失值样本中取某一属性值 $a^{v}$ 的样本所占比例.
更详细的说:

详见:[决策树(decision tree)——缺失值处理](https://blog.csdn.net/zhaomengszu/article/details/80775554)
---
转载:[决策树—分类](https://zhuanlan.zhihu.com/p/42164714)