GBDT - 数据挖掘

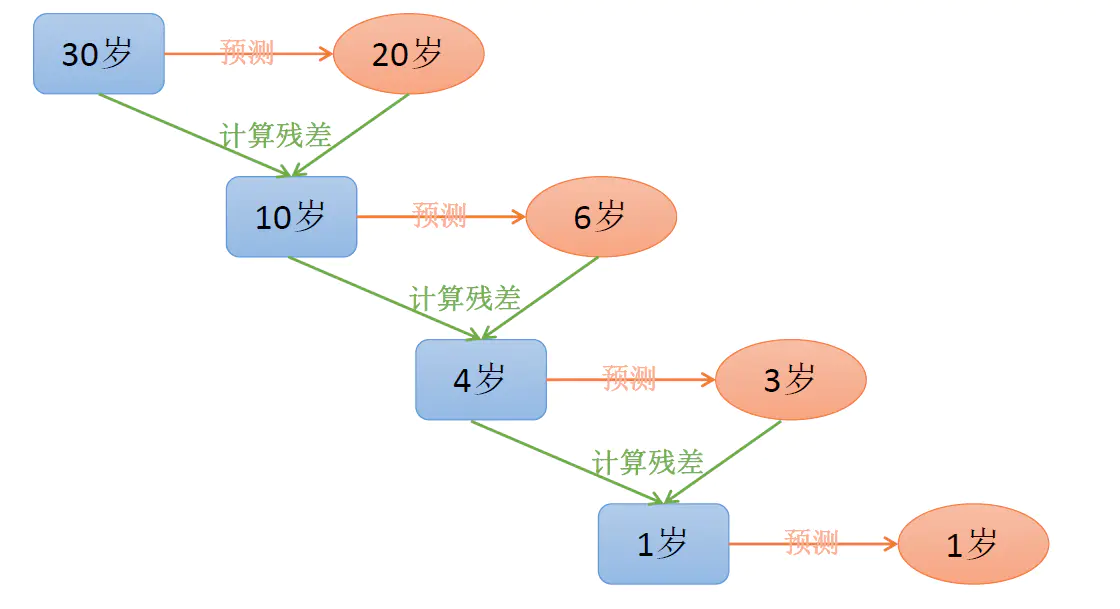
>前言：虽然文无第一武无第二，在机器学习领域并没有什么最厉害的模型这一说。但在深度学习兴起和流行之前，GBDT的确是公认效果最出色的几个模型之一。虽然现在已经号称进入了深度学习以及人工智能时代，但是GBDT也没有落伍，它依然在很多的场景和公司当中被广泛使用。也是面试当中经常会问到的模型之一。 GBDT 直观理解：每一轮预测和实际值有残差，下一轮根据残差再进行预测，最后将所有预测相加，就是结果。 ::: hljs-center ![image.png](https://cos.easydoc.net/17082933/files/ke8he4lb.png) ::: # GBDT基础概念 GBDT的英文原文是Gradient Boosting Decision Tree，即**梯度提升决策树**。从它的英文表述我们可以看出来，GBDT的**基础还是决策树**。决策树我们在之前的文章当中曾经有过详细的讨论，我们这里就不再赘述了。在GBDT当中用到的主要是决策树的**CART算法**，在CART算法当中，我们每次都会**选择一个特征并且寻找一个阈值进行二分**。将样本根据阈值分成小于等于阈值的以及大于阈值的两个部分，在**CART树当中，同一个特征可以重复使用**，其他类似的ID3和C4.5都没有这个性质。另外一个关键词是**Boosting**，Boosting表示一种集成模型的训练方法，我们之前在介绍AdaBoost模型的时候曾经提到过。它最大的特点就是会**训练多个模型**，通过**不断地迭代来降低整体模型的偏差**。比如在Adaboost模型当中，会设置多个弱分类器，根据这些分类器的表现我们会给与它们不同的权值。通过这种设计尽可能让效果好的分类器拥有高权重，从而保证模型的拟合能力。 **但GBDT的Boosting方法与众不同**，它是一个由多棵CART决策回归树构成的加法模型。我们可以简单理解成最后整个模型的预测结果是**所有回归树预测结果的和**，理解了这一点对于后面理解梯度和残差非常重要。我们可以试着写一下GBDT的预测公式： ::: hljs-center $f_{M}(x)=\sum_{i=1}^{M} T\left(x, \theta_{i}\right)$ ::: 公式中的M表示CART树的个数，$T(x, \theta_{i})$表示第i棵回归树对于样本的预测结果，其中的 $\theta$ 表示每一棵回归树当中的参数。所以整个过程就和我刚才说的一样，GBDT模型最后的结果是**所有回归树预测结果的加和。** # GBDT回归 ## 梯度和残差下面我们要介绍到梯度和残差的概念了，我们先来回顾一下线性回归当中梯度下降的用法。在线性回归当中我们使用梯度下降法是为了**寻找最佳的参数**，使得损失函数最小。实际上目前绝大多数的模型都是这么做的，计算梯度的目的是为了调整参数。但是GBDT不同，**计算梯度是为了下一轮的迭代**，这句话非常关键，一定要理解。我们来举个例子，假设我们用线性回归 $y=\theta x+b$ 拟合一个值，这里的目标y是20。我们当前的[公式]得到的 $\theta$ 是 10，那么我们应该计算梯度来调整参数 $\hat{y}$，明显应该将它调大一些从而降低偏差。但是GBDT不是这么干的，同样假设我们第一棵回归树得到的结果也是10，和真实结果相差了10，我们一样来计算梯度。在回归问题当中，我们通常使用**均方差MSE**作为损失函数，那么我们可以来算一下这个函数的梯度。我们先写出损失函数的公式： ::: hljs-center $L=\frac{1}{2}\left(y_{i}-f\left(x_{i}\right)\right)^{2}$ ::: L关于 $f(x_i)$ 的负梯度值刚好等于 $y_{i}-f(x_i)$ ，看起来**刚好是我们要预测的目标值减去之前模型预测的结果**。这个值也就是我们常说的残差。我们用 $r_{mi}$ 表示第$m$棵回归树对于样本i的训练目标，它的公式为： ::: hljs-center $r_{mi}=y_{i}-f(x_i)$ ::: 从直观上来讲究很简单了，我们要预测的结果是20，第一棵树预测了10，相差还剩10，于是我们用第二棵树来逼近。第二棵树预测了5，相差变成了5，我们继续创建第三棵树…… 一直到我们已经逼近到了非常接近小于我们设定的阈值的时候，或者子树的数量达到了上限，这个时候模型的训练就停止了。这里要注意，**不能把残差简单理解成目标值和 $f(x_i)$ 的差值**，它本质是由损失函数计算负梯度得到的。 ## 训练过程我们再把模型训练的整个过程给整理一下，把所有的细节串联起来。首先我们先明确几个参数，M表示决策树的数量。$f_m(x_i)$ 表示第m轮训练之后的整体，$f_m(x_i)$即为最终输出的GBDT模型。 1. **初始化** 首先，我们创建第一棵回归树即 $f_1(x)$ ，在回归问题当中，它是直接用回归树拟合目标值的结果，所以： ::: hljs-center $f_{1}(x)=\underset{c}{\arg \min } \sum_{i=1}^{N} L\left(y_{i}, c\right)$ ::: 2. **迭代** - 对于第2到第m棵回归树，我们要计算出每一棵树的训练目标，也就是前面结果的残差： ::: hljs-center $r_{m i}=-\left[\frac{\partial L\left(y_{i}, f\left(x_{i}\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f(x)=f_{m-1}(x)}$ ::: - 对于当前第m棵子树而言，我们需要遍历它的可行的切分点以及阈值，找到最优的预测值c对应的参数，使得尽可能逼近残差，我们来写出这段公式： ::: hljs-center $c_{m j}=\underset{c}{\arg \min } \sum_{x_{i} \in R_{m j}} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+c\right)$ ::: - 这里的 $R_{mj}$ 指的是第m棵子树所有的划分方法中叶子节点预测值的集合，也就是**第m棵回归树可能达到的预测值**。其中j的范围是1,2,3...J。接着，我们更新 $f_{m}(x)=f_{m-1}(x)+\sum_{j=1}^{J} c_{m j} I\left(x \in R_{m j}\right)$ ，这里的I是一个函数，如果样本落在了$R_{mj}$节点上，那么I=1，否则I=0。 3. **最后我们得到回归树** ::: hljs-center $F(x)=f_{M}(x)=\sum_{m=1}^{M} f_{m}(x)=\sum_{m=1}^{M} \sum_{j=1}^{J} c_{m j} I\left(x \in R_{m j}\right)$ ::: 上述的公式看起来有些复杂，其实就是我们借助 $c_{mj}$ 和$I$把回归树的情况表示了出来而已。因为我们训练模型最终希望得到的其实是模型的参数，对于回归树而言，它的参数表示比较复杂，所以看起来可能会有些迷惑。我们可以简单一点理解，GBDT就是利用的加法模型训练多棵回归树，预测的结果是这些回归树的和。而每一棵回归树的训练目标都是之前模型的残差。 ## Shrinkage Shinkage是一种优化**避免GBDT陷入过拟合的方法**，这个方法的本质是**减小每一次迭代对于残差的收敛程度**，认为每一次逼近少一些多次收敛的效果好于一次逼近很多，逼近次数较少的结果。具体的表现措施就是给我们的每一棵回归树的结果**乘上一个类似于学习率的参数**，通过增大回归树的个数来弥补。说白了就和梯度下降的时候我们乘上学习率是一样的，只不过在梯度下降的问题当中，我们明确知道不乘学习率的话会陷入震荡无法收敛的问题。而在GBDT当中，Shrinkage的机制并没有一个明确的证明或者是感性的认识，它的效果**更多是基于经验的**。我们写一下加上Shrinkage之后的方程来做个对比： ::: hljs-center $f_{m}(x)=f_{m-1}(x)+\gamma \sum_{j=1}^{J} c_{m j} I\left(x \in R_{m j}\right)$ ::: 这里的 $\gamma$ 就是我们的Shrinkage的参数，**一般取值在0.001到0.01之间。** ## 总结到这里，关于GBDT模型的基本原理就算是介绍完了。如果你对于之前关于决策树的相关文章都认真阅读的话，相信理解GBDT对于你来说应该不是一件困难的事。如果你没有读过或者是错过了之前的文章的话，可以看一下文末的相关阅读的部分，回顾一下之前的内容。 GBDT最大的创新就在于，将传统的调整参数来降低梯度的过程转化成了创建新的树模型来逼近，我第一次看到的时候深深为之惊艳。和传统的模型相比，由于GBDT是综合了多个分类器的结果，所以更加不容易陷入过拟合，并且对于一些复杂的场景的拟合效果会更好。今天我们介绍的只是最基本的回归问题当中的解法，在分类问题当中，公式会稍稍有些不同，这部分内容我们放在下篇文章当中。转载：[机器学习 | 详解GBDT梯度提升树原理，看完再也不怕面试了](https://zhuanlan.zhihu.com/p/169568445) --- **但是这就又有一个问题**，如果是回归问题那还好说，如果是**分类问题那怎么办？** 难道分类结果也能加和吗？其实也是可以的，我们知道在逻辑回归当中，我们用到的公式是$\hat{y}=\frac{1}{1+e^{-\theta x}}$，这个式子的结果表示样本的类别是1的概率。我们当然不能直接来拟合这个概率，但是我们可以用**加和的方式来拟合 $\theta x$ 的结果**，这样我们就间接得到了概率。 **往下看**： # GBDT分类 ## 逻辑回归损失函数在我们开始GBDT模型原理的讲解和推导之前，我们先来回顾一下逻辑回归当中的相关公式和概念。首先，我们先来写出逻辑回归的预测函数： ::: hljs-center $h_{\theta}(x)=\frac{1}{1+e^{-\theta^{T} x}}$ ::: 图像画出来是这样的，其中的 $h_{\theta}(x)$ 表示表示了模型预测x这个样本属于类别1的概率。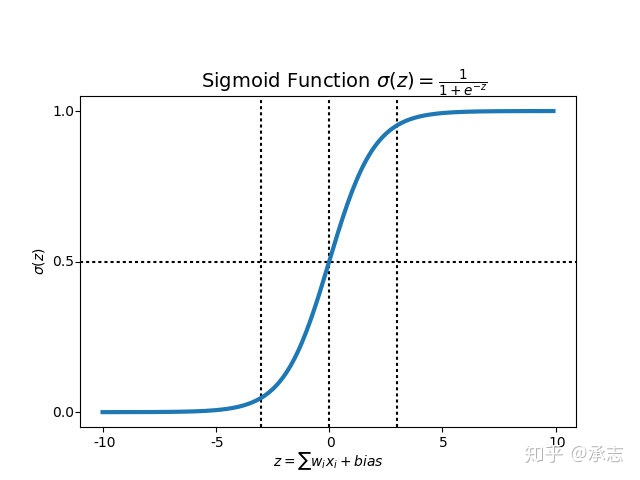 ::: hljs-center ![image.png](https://cos.easydoc.net/17082933/files/ke8iatin.png) ::: 在二分类问题当中，只有0和1两个类别，两个类别的概率只和为1。所以我们可以得到 $P(y=0 \mid x ; \theta)=1-h_{\theta}(x)$ 。我们希望模型在y=0的时候，使得$1-h_{\theta}(x)$尽量大，否则则使得$h_{\theta}(x)$尽量大，我们用指数的形式把两者综合写出了它的损失函数L。 ::: hljs-center $l(\theta)=-h_{\theta}(x)^{y}\left(1-h_{\theta}(x)\right)^{1-y}$ ::: 这个值涉及到指数，计算起来不太方便，所以我们会对它求对数进行简化。等式两边都取对数之后，可以得到： ::: hljs-center $L(\theta)=\log (l(\theta))=-\sum_{i=1}^{N}\left[y_{i} \log h_{\theta}\left(x_{i}\right)+\left(1-y_{i}\right) \log \left(1-h_{\theta}\left(x_{i}\right)\right)\right]$ ::: 这个就是逻辑回归损失函数的由来。 ## GBDT二分类我们将GBDT模型应用在二分类的场景当中的原理其实和逻辑回归一样，只不过在逻辑回归当中 $h_{\theta}x$ 是一个线性函数，而在GBDT当中，$h_{\theta}=\sum_{m=1}^{M} f_{m}(x)$ 是一个**加法模型**。在GBDT的回归问题当中，$h_{\theta}x$就是GBDT产出的最后结果，而在二分类问题当中，我们还需要对这个结果加上一个sigmoid函数。我们令上面的$h_{\theta}$为 $F_M(x)$ ，所以模型可以表达为： ::: hljs-center $P(y=1 \mid x)=\frac{1}{1+e^{-F_{M}(x)}}$ ::: 我们把这个式子带入逻辑回归的损失函数当中，可以得到： ::: hljs-center $\begin{aligned} L\left(x_{i}, y_{i} \mid F_{M}(x)\right) &=-y_{i} \log \left(\frac{1}{1+e^{-F_{M}\left(x_{i}\right)}}\right)-\left(1-y_{i}\right) \log \left(1-\frac{1}{1+e^{-F_{M}\left(x_{i}\right)}}\right) \\ &=y_{i} \log \left(1+e^{-F_{M}\left(x_{i}\right)}\right)+\left(1-y_{i}\right)\left[F_{M}\left(x_{i}\right)+\log \left(1+e^{-F_{M}\left(x_{i}\right)}\right)\right] \end{aligned}$ ::: 我们对损失函数计算负梯度，也即计算 $L\left(x, y \mid F_{M}(X)\right)$ 对 $F_{M}(x)$ 的偏导： ::: hljs-center $-\frac{\partial L}{\partial F_{M}}=y_{i}-\frac{1}{1+e^{-F_{M}(x)}}=y_{i}-\hat{y}_{i}$ ::: 这个负梯度也就是我们常说的**残差**，这个残差的结果和我们之前在回归问题当中的推导结果非常近似。它表示预测概率和真实概率的概率差，这个残差就是下一棵CART树的训练目标。 ## 训练过程我们再把模型训练的整个过程给整理一下，把所有的细节串联起来。首先我们先明确几个参数，M表示决策树的数量。$F_{m}\left(x_{i}\right)$ 表示第m轮训练之后的整体，$F_{m}\left(x_{i}\right)$ 即为最终输出的GBDT模型。 **1、初始化** 首先，我们创建第一棵回归树即$f_1(x)$，在二分类问题当中，它是先验信息，所以： ::: hljs-center $f_{1}(x)=\log \frac{p 1}{1-p 1}$ ::: $p1$表示**样本中类别1的比例** - 对于第2到第m棵回归树，我们要计算出每一棵树的训练目标，也就是前面结果的残差： ::: hljs-center $r_{m i}=-\left[\frac{\partial L\left(y_{i}, f\left(x_{i}\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f(x)=f_{m-1}(x)}=y_{i}-\hat{y}_{i}$ ::: - 对于当前第m棵子树而言，我们需要遍历它的可行的切分点以及阈值，找到最优的预测值c对应的参数，使得尽可能逼近残差，我们来写出这段公式： ::: hljs-center $c_{m j}=\underset{c}{\arg \min } \sum_{x_{i} \in R_{m j}} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+c\right)$ ::: 这里的 $R_{m j}$ 指的是第m棵子树所有的划分方法中叶子节点预测值的集合，也就是**第m棵回归树可能达到的预测值**。其中j的范围是1,2,3...J。接着，我们更新 ::: hljs-center $f_{m}(x)=f_{m-1}(x)+\sum_{j=1}^{J} c_{m j} I\left(x \in R_{m j}\right)$ ::: ，这里的$I$是一个函数，如果样本落在了 $R_{m j}$ 节点上，那么$I=1$，否则$I=0$。 **2、我们得到** ::: hljs-center $F_{M}(x)=f_{M}(x)=\sum_{m=1}^{M} f_{m}(x)=\sum_{m=1}^{M} \sum_{j=1}^{J} c_{m j} I\left(x \in R_{m j}\right)$ ::: **3、某条样本类别为1的概率为：** ::: hljs-center $P\left(x_{i}\right)=\frac{1}{1+e^{-F_{M}\left(x_{i}\right)}}$ ::: ## 多分类问题二分类的问题解决了，多分类也并不困难，其实也只是二分类的一个简单拓展。我们假设样本的类别数量是k，那么我们需要**k个不同的树集合**来拟合每个类别的概率。我们写出类别q的概率的公式： ::: hljs-center $P(y=q \mid x)=\frac{e^{F_{q}(x)}}{\sum_{i=1}^{k} e^{F_{i}(x)}}$ ::: softmax函数的损失函数为：$L=-\sum y_{i} \log \left(P\left(y_{i} \mid x\right)\right)$，虽然从公式里看这是一个求和值，但是对于多分类问题来说，**只会有一个类别为1**，其余均为0，所以只会有一项不为0，我们假设这一项为q。我们代入求出它的负梯度： ::: hljs-center $-\frac{\partial L}{\partial F_{q}}=y_{q}-\frac{e^{F_{q}(x)}}{\sum_{i=1}^{k} e^{F_{i}(x)}}=y_{q}-\hat{y}_{q}$ ::: 可见在多分类问题当中，这k个树集合同样是拟合真实的样本标签与预测的概率的差值，本质上和二分类问题是一样的。 ## 总结到这里，关于GBDT在分类场景当中的原理我们也介绍完了。其实整篇推倒下来，无论是过程和结果都和回归问题大同小异。只不过由于分类问题用到了sigmoid函数，使得计算偏导以及残差的过程稍稍复杂了一些，其他并没有什么本质差别。从今天的文章当中我们也可以看出来，GBDT模型适用的范围很广，回归、二分类以及多分类问题都可以适用，是一个非常强大的模型。也正因此，它在深度学习兴起之前一度非常流行，基于它也衍生出了许多的改进的版本和应用。比如XGboost，GBDT + LR等等。也因此在面试的时候经常会问到其中的问题，如果有准备面试的同学，建议一定要将原理吃透哦。 --- 转载：[机器学习 | 详解GBDT在分类场景中的应用原理与公式推导](https://zhuanlan.zhihu.com/p/187288784)