Gradient Boosting
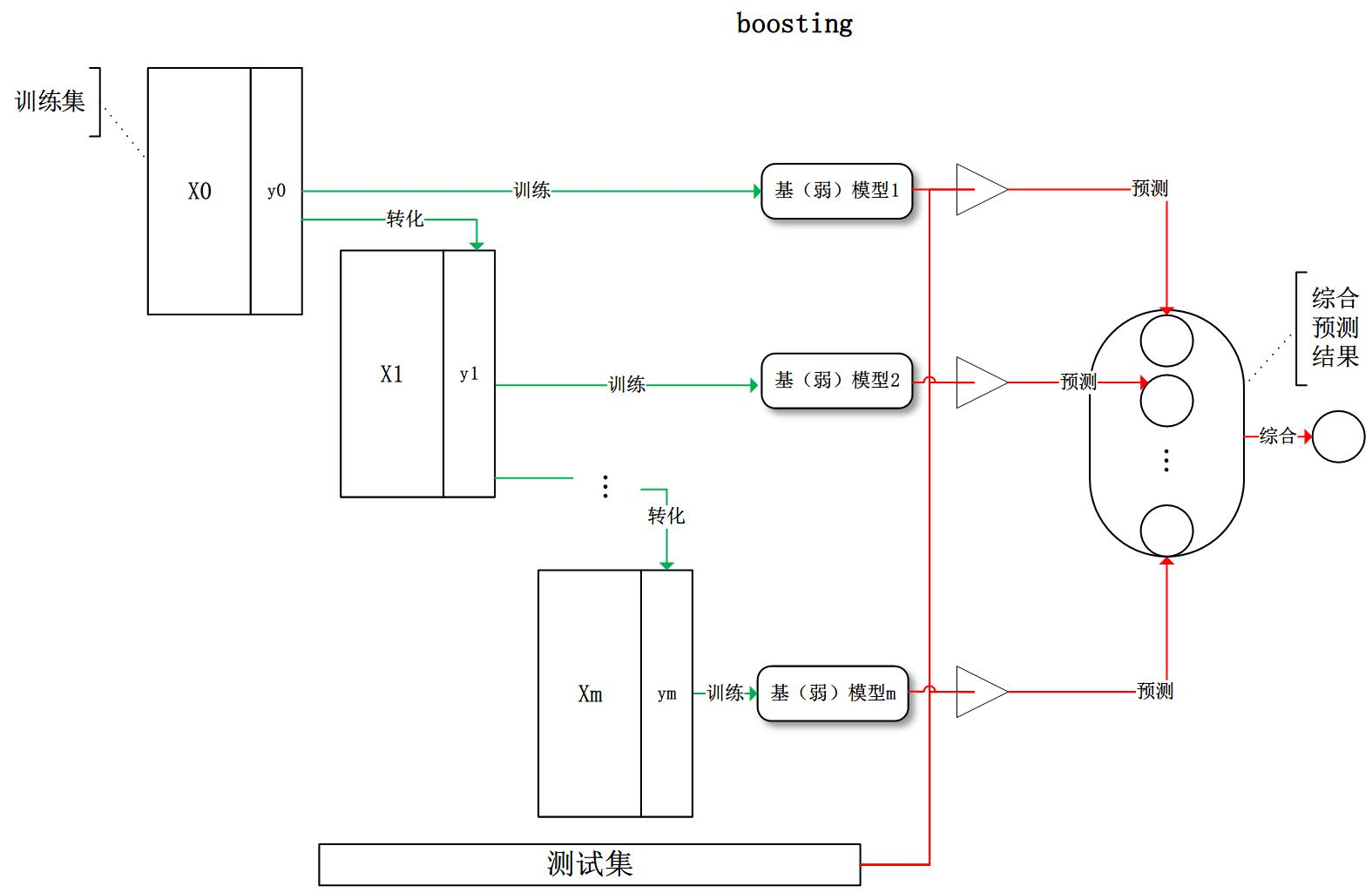
**boosting**:训练过程为阶梯状,基模型按次序一一进行训练(实现上可以做到并行),基模型的训练集按照某种策略每次都进行一定的转化。对所有基模型预测的结果进行线性综合产生最终的预测结果:
::: hljs-center
:::
# Gradient Boosting
Gradient Boosting 和其它 Boosting 算法一样,通过将表现一般的数个模型(通常是深度固定的决策树)组合在一起来集成一个表现较好的模型。抽象地说,模型的训练过程是对任意可导目标函数的优化过程。通过反复地选择一个指向负梯度方向的函数,该算法可看作在函数空间里对目标函数进行优化。因此可以说 Gradient Boosting = Gradient Descend + Boosting。
和 AdaBoost 一样,Gradient Boosting 也是重复选择一个表现一般的模型,每次基于先前的模型的表现进行调整。不同的是,AdaBoost 是通过提升错误分类数据点的权重来定位模型的不足,而Gradient Boosting 是通过计算梯度(gradient)来定位模型的不足。因此相比 AdaBoost,Gradient Boosting 可以使用更多种类的目标函数(损失函数)。
有一组训练数据集$T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{N}, y_{N}\right)\right\},$ 其中 $x_{i} \in \mathcal{X} \subseteq \mathbb{R}^{n}, y_{i} \in \mathcal{Y}=\{-1,+1\}$和一个基础模型 $F$。对基于 Gradient Boosting 框架的模型的进行调试时,我们会遇到一个重要的概念:**损失函数**。在本节中,我们将把损失函数的“今生来世”讲个清楚!基于 boosting 框架的整体模型可以用**线性组成式**来描述,其中 $h_i(x)$ 为基模型与其权值的乘积:
::: hljs-center
$F(x)=\sum_{i}^{m} h_{i}(x)$
:::
根据上式,整体模型的训练目标是使**预测值 $F(x)$** 逼近**真实值 $y$**,也就是说要让每一个基模型的预测值逼近各自要预测的部分真实值。由于要同时考虑所有基模型,导致了整体模型的训练变成了一个非常复杂的问题。所以,研究者们想到了一个贪心的解决手段:每次只训练一个基模型。那么,现在改写整体模型为迭代式:
::: hljs-center
$F^{i}(x)=F^{i-1}(x)+h_{i}(x)$
:::
这样一来,每一轮迭代中,只要集中解决一个基模型的训练问题:使 $F^i(x)$ 逼近真实值 $y$ 。
## 拟合残差
使 $F^i(x)$ 逼近真实值,其实就是使 $h_i(x)$ 逼近真实值和上一轮迭代的预测值 $F^{i-1}(x)$ 之差,即残差 $y-F^{i-1}(x)$。**最直接的做法是构建基模型来拟合残差**,在[GBDT(MART) 迭代决策树入门教程 | 简介](https://blog.csdn.net/w28971023/article/details/8240756)中,作者举了一个生动的例子来说明通过基模型拟合残差,最终达到整体模型 逼近真实值。
研究者发现,残差其实是**最小均方损失函数**的关于预测值的反向梯度:
::: hljs-center
$-\frac{\partial\left(\frac{1}{2} \cdot\left(y-F^{i-1}(x)\right)^{2}\right)}{\partial F^{i-1}(X)}=y-F^{i-1}(x)$
:::
**因此,在这里拟合残差实际上就是拟合最小均方损失函数的负梯度,当然,当损失函数不是最小均方时残差并不一定等于负梯度!** 也就是说,若 $F^{i-1}(x)$ 加上拟合了反向梯度的 $h_i(x)$ 得到 $F^{i}(x)$,该值可能将导致平方差损失函数降低,预测的准确度提高!我们显然是在通过梯度下降法对模型参数进行更新,这样理解的好处在于我们可以把这一算法推广到其他的损失函数上。
**要注意,回归问题损失函数并不一定会使用最小均方损失函数。最小均方损失函数的优点是便于理解和实现,缺点在于对于异常值,它的鲁棒性较差,如下图(标星号的数据为异常值):**
|$x_i$|0.5|1.2|2|5*|
|-|-|-|-|-|
|F|0.6|1.4|1.5|1.7|
|Square loss|0.005|0.02|0.125|5.445|
一个异常值造成的损失由于二次幂而被过分放大,会影响到最后得到的模型在测试集上的表现。
因此我们有时候也会选择其他的损失函数,如 Absolute loss 或 Huber loss:
::: hljs-center
$L_{a b s o l u t e}(y, F)=|y-f|$
:::
::: hljs-center
$L_{h u b e r}(y, F)=\left\{\begin{array}{r}\frac{1}{2}(y-F)^{2},|y-F| \leq \delta \\ \delta\left(|y-F|-\frac{\delta}{2}\right),|y-F| \geq \delta\end{array}\right.$
:::
|$x_i$|0.5|1.2|2|5*|
|-|-|-|-|-|
|F|0.6|1.4|1.5|1.7|
|Square loss|0.005|0.02|0.125|5.445|
|Absolute loss|0.1|0.2|0.5|3.3|
|Huber loss(δ=0.5)|0.005|0.02|0.125|1.525|
梯度下降法的思想使得我们可以非常轻易地改用不同的损失函数设计 Gradient Boosting 算法。
## 拟合反向梯度
### 契机:引入任意损失函数
引入任意损失函数后,我们可以定义整体模型的迭代式如下:
::: hljs-center
$F^{i}(x)=F^{i-1}(x)+\arg \min _{h \in H} \sum_{j}^{n} L\left(y_{j}, F^{i-1}\left(x_{j}\right)+h_{i}\left(x_{j}\right)\right)$
:::
在这里,损失函数被定义为泛函。
### 难题一:任意损失函数的最优化
对任意损失函数(且是泛函)的最优化是困难的。我们需要打破思维的枷锁,将整体损失函数 L' 定义为n元普通函数(n为样本容量),损失函数 L 定义为2元普通函数(记住!!!这里的损失函数不再是泛函!!!):
::: hljs-center
$L^{\prime}\left(F^{i-1}\left(x_{i}\right), F^{i-1}\left(x_{2}\right), \ldots, F^{i-1}\left(x_{n}\right)\right)=\sum_{j}^{n} L\left(y_{j}, F^{i-1}\left(x_{j}\right)\right)$
:::
我们不妨使用梯度最速下降法来解决整体损失函数 L' 最小化的问题,先求整体损失函数的反向梯度:
::: hljs-center
$-\frac{\partial L^{\prime}\left(F^{i-1}\left(x_{i}\right), F^{i-1}\left(x_{2}\right), \ldots, F^{i-1}\left(x_{n}\right)\right)}{\partial F^{i-1}\left(x_{j}\right)}=-\frac{\partial L\left(y_{j}, F^{i-1}\left(x_{j}\right)\right)}{\partial F^{i-1}\left(x_{j}\right)}$
:::
假设已知样本 $x$ 的当前预测值为 $F^{i-1}(x)$ ,下一步将预测值按照反向梯度,依照步长为$\gamma_i$ ,进行更新:
::: hljs-center
$F^{i}(x)=F^{i-1}(x)-\gamma_{i} \cdot \frac{\partial L\left(y_{j}, F^{i-1}\left(x_{j}\right)\right)}{\partial F^{i-1}\left(x_{j}\right)}$
:::
步长 $\gamma_i$ 不是固定值,而是设计为:
::: hljs-center
$\gamma_{i}=\arg \min _{\gamma} \sum_{j}^{n} L\left(y_{j}, F^{i-1}(x)-\gamma \cdot \frac{\partial L\left(y_{j}, F^{i-1}\left(x_{j}\right)\right)}{\partial F^{i-1}\left(x_{j}\right)}\right)$
:::
### 难题二:无法对测试样本计算反向梯度
问题又来了,由于**测试样本中 $y$ 是未知的**,所以无法求反向梯度。这正是 Gradient Boosting 框架中的基模型闪亮登场的时刻!在第 $i$ 轮迭代中,我们创建**训练集**如下:
::: hljs-center
$\left\{\left(x_{j},-\frac{\partial L\left(y_{j}, F^{i-1}\left(x_{j}\right)\right)}{\partial F^{i-1}\left(x_{j}\right)}\right)\right\}_{j}^{n}$
:::
也就是说,让**基模型**拟合反向梯度函数,这样我们就可以做到只输入 $x$ 这一个参数,就可求出其对应的反向梯度了(当然,通过基模型预测出来的反向梯度并不是准确的,这也提供了泛化整体模型的机会)。
综上,假设第 $i$ 轮迭代中,根据新训练集训练出来的基模型为 $f_i(x)$ ,那么最终的迭代公式为:
::: hljs-center
$F^{i}(x)=F^{i-1}(x)-\gamma_{i} \cdot f_{i}(x)$
$\gamma_{i}=\arg \min _{\gamma} \sum_{j}^{n} L\left(y_{j}, F^{i-1}(x)-\gamma \cdot f_{i}(X)\right)$
:::
## 常见的损失函数
**ls**:最小均方回归中用到的损失函数。在之前我们已经谈到,从拟合残差的角度来说,残差即是该损失函数的反向梯度值(所以又称反向梯度为伪残差)。不同的是,从拟合残差的角度来说,步长是无意义的。该损失函数是sklearn中Gradient Tree Boosting回归模型默认的损失函数。
**deviance**:逻辑回归中用到的损失函数。熟悉逻辑回归的读者肯定还记得,**逻辑回归本质是求极大似然解**,其认为样本服从几何分布,样本属于某类别的概率可以 logistic 函数表达。所以,如果该损失函数可用在多类别的分类问题上,故其是 sklearn 中 Gradient Tree Boosting 分类模型默认的损失函数。
**exponential**:指数损失函数,表达式为:
::: hljs-center
$L\left(y_{j}, F^{i-1}\left(x_{j}\right)\right)=e^{\left(-y_{j} \cdot F^{i-1}\left(x_{j}\right)\right)}$
:::
对该损失函数求反向梯度得:
::: hljs-center
$-\frac{\partial L\left(y_{j}, F^{i-1}\left(x_{j}\right)\right)}{\partial F^{i-1}\left(x_{j}\right)}=y_{j} \cdot e^{\left(-y_{j} \cdot F^{i-1}\left(x_{j}\right)\right)}$
:::
这时,在第 $i$ 轮迭代中,新训练集如下:
::: hljs-center
$\left\{\left(x_{j}, y_{j} \cdot e^{\left(-y_{j} \cdot F^{i-1}\left(x_{j}\right)\right)}\right)\right\}_{j}^{n}$
:::
脑袋里有什么东西浮出水面了吧?让我们看看Adaboost算法中,第 $i$ 轮迭代中第 $j$ 个样本权值的更新公式:
::: hljs-center
$\omega_{i, j}=\frac{e^{\left(-y_{j} \cdot F^{i-1}\left(x_{j}\right)\right)}}{\sum_{i}^{n} e^{\left(-y_{j} \cdot F^{i-1}\left(x_{j}\right)\right)}}$
:::
样本的权值什么时候会用到呢?计算第 $i$ 轮损失函数的时候会用到
::: hljs-center
$L\left(y_{j}, F^{i}\left(x_{j}\right)\right)=e^{\left(-y_{j} \cdot F^{i}\left(x_{j}\right) \cdot \frac{\left.e^{\left(-y_{j} \cdot F^{i-1}\left(x_{j}\right)\right.}\right)}{\Sigma_{i}^{n} e^{\left(-y_{j} \cdot F^{i-1}\left(x_{j}\right)\right)}}\right)}$
:::
让我们再回过头来,看看使用指数损失函数的 Gradient Boosting 计算第 $i$ 轮损失函数:
::: hljs-center
$L\left(y_{j}, F^{i}\left(x_{j}\right)\right)=e^{\left.\left(-y_{j} \cdot F^{i}\left(x_{j}\right) \cdot e^{\left(-y_{j} \cdot F^{i-1}\left(x_{j}\right)\right.}\right)\right)}$
:::
天呐,两个公式就差了一个对**权值的归一项**。这并不是巧合,当损失函数是指数损失时,Gradient Boosting 相当于二分类的 Adaboost 算法。是的,**指数损失仅能用于二分类的情况**。
## 步子太大容易扯着蛋:缩减
缩减也是一个相对显见的概念,也就是说使用 Gradient Boosting 时,每次学习的步长缩减一点。这有什么好处呢?缩减思想认为每次走一小步,多走几次,更容易逼近真实值。如果步子迈大了,使用最速下降法时,容易迈过最优点。将缩减代入迭代公式:
::: hljs-center
$F^{i}(x)=F^{i-1}(x)-v \cdot \gamma \cdot f_{i}(x), 0<v \leq 1$
:::
缩减需要配合**基模型数**一起使用,当缩减率 $v$ 降低时,基模型数要配合增大,这样才能提高模型的准确度。
## 初始模型
还有一个不那么起眼的问题,初始模型 $F^0(x)$ 是什么呢?如果没有定义初始模型,整体模型的迭代式一刻都无法进行!所以,我们定义初始模型为:
::: hljs-center
$F^{0}(x)=\arg \min _{\gamma} \sum_{j}^{n} L\left(y_{j}, \gamma\right)$
:::
根据上式可知,对于不同的损失函数来说,初始模型也是不一样的。对所有的样本来说,根据初始模型预测出来的值都一样。
## Gradient Tree Boosting
终于到了备受欢迎的Gradient Tree Boosting模型了!但是,可讲的却已经不多了。我们已经知道了该模型的基模型是树模型,并且可以通过对特征的随机抽样进一步减少整体模型的方差。我们可以在维基百科的Gradient Boosting词条中找到其伪代码实现。
## 小结
到此,读者应当很清楚 Gradient Boosting 中的损失函数有什么意义了。要说偏差描述了模型在训练集准确度,则损失函数则是描述该准确度的间接量纲。也就是说,模型采用不同的损失函数,其训练过程会朝着不同的方向进行!