逻辑回归
机器学习解决的问题,大体上就是两种:数值预测和分类。前者一般采用的是回归模型,比如最常用的线性回归;后者的方法则五花八门,决策树,kNN,支持向量机,朴素贝叶斯等等模型都是用来解决分类问题的。其实,两种问题从本质上讲是一样的:都是通过对已有数据的学习,构建模型,然后对未知的数据进行预测,若是连续的数值预测就是回归问题,若是离散的类标号预测,就是分类问题。
这里面有一类比较特殊的算法,就是逻辑回归(logistic regression)。它叫“回归”,可见基本思路还是回归的那一套,同时,逻辑回归又是标准的解决分类问题的模型。换句话说,逻辑回归是用与回归类似的思路解决了分类问题。
# 阶跃函数
现在有n个数据元组$\{X_1,X_2,…,X_n\}$,每个数据元组对应了一个类标号$y_i$,同时每个数据元组$X_i$有$m$个属性$\{x_{i1},x_{i2},…,x_{im}\}$。假设现在面临的是一个简单的二分类问题,类标号有0,1两种。如果用简单的回归方法对已知数据进行曲线拟合的话,我们会得到如下的曲线方程(曲线拟合的方法后面会说到):
::: hljs-center
$z=f(X)=w_0+w_1x_1+w_2x_2+⋯+w_mx_m$
:::
注:并不是说逻辑回归只能解决二分类问题,但是用到多分类时,算法并没有发生变化,只是用的次数更多了而已。
**实际上,逻辑回归分类的办法与SVM是一致的,都是在空间中找到曲线,将数据点按相对曲线的位置,分成上下两类**。也就是说,对于任意测试元组 $X^*$ ,$f(X^*)$可以根据其正负性而得到类标号。那换句话说,**直接依靠拟合曲线的函数值是不能得到类标号的,还需要一种理想的“阶跃函数”,将函数值按照正负性分别映射为0,1类标号**。这样的阶跃函数$ϕ(z)$如下表示:
::: hljs-center
$\phi(z)=\left\{\begin{aligned} 0, & z<0 \\ 0.5, & z=0 \\ 1, & z>0 \end{aligned}\right.$
:::
然而,直接这样设计阶跃函数不方便后面的优化计算,因为函数值不连续,无法进行一些相关求导。所以,逻辑回归中,大家选了一个统一的函数,也就是$Sigmoid$函数,如下公式所示:
::: hljs-center
$\phi(z)=\frac{1}{1+e^{-z}}$
:::
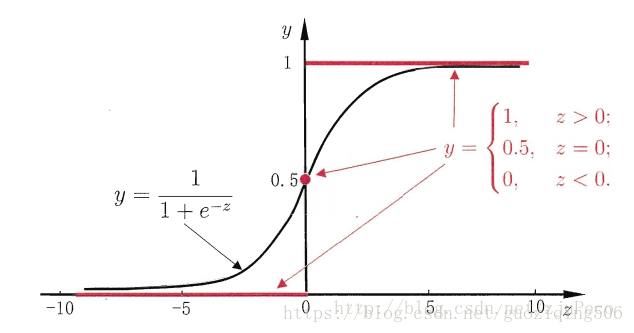
$Sigmoid$函数的图像如下图所示,当$z>$ 0时,$Sigmoid$函数大于0.5;当$z<0$时,$Sigmoid$函数小于0.5。所以,我们可以将拟合曲线的函数值带入Sigmoid函数,观察 $ϕ(z)$ 与0.5的大小确定其类标号。
::: hljs-center
:::
**$Sigmoid$函数还有一个好处,那就是因为其取值在0,1之间。所以可以看做是测试元组属于类1的后验概率,即$p(y=1|X)$。** 其实这一点从图像也可以看出来:$z$的值越大,表明元组的空间位置距离分类面越远,他就越可能属于类1,所以图中$z$越大,函数值也就越接近1;同理,$z$越小,表明元组越不可能属于类1.
# 代价函数
阶跃函数告诉我们,当得到拟合曲线的函数值时,如何计算最终的类标号。但是核心问题仍然是这个曲线如何拟合。既然是回归函数,我们就模仿线性回归,用误差的平方和当做代价函数。代价函数如**公式(2)** 所示:
::: hljs-center
$J(w)=\sum_{i=1}^{n} \frac{1}{2}\left(\phi\left(z_{i}\right)-y_{i}\right)^{2}$
:::
其中,$z_{i}=W^{T} X_{i}+w_{0}$,$y_i$为$X_i$真实的类标号。按说此时可以对代价函数求解最小值了,但是如果你将 $\phi(z)=\frac{1}{1+e^{-z}}$ 带入公式(2)的话,那么当前代价函数的图像是一个非凸函数,非凸函数有不止一个极值点,导致不容易做最优化计算。也就是说,公式(2)的这个代价函数不能用。
关于凸函数的相关知识可以参考博客: [最大化期望算法(EM)详解](https://blog.csdn.net/guoziqing506/article/details/81274276)
那自然要想办法设计新的代价函数。我们在上面说了,$ϕ(z)$的取值可以看做是测试元组属于类1的后验概率,所以可以得到下面的结论:
::: hljs-center
$p(y=1 \mid X ; W)=\phi(z)$
$p(y=0 \mid X ; W)=1-\phi(z)$
:::
更进一步,上式也可以这样表达:
::: hljs-center
$p(y \mid X ; W)=\phi(z)^{y}(1-\phi(z))^{1-y}$
:::
上面这个公式表达的含义是在参数$W$下,元组类标号为$y$的后验概率。假设现在已经得到了一个抽样样本,那么联合概率 $\prod_{i=1}^{n} p\left(y_{i} \mid X_{i} ; W\right)$ 的大小就可以反映模型的代价:联合概率越大,说明模型的学习结果与真实情况越接近;联合概率越小,说明模型的学习结果与真实情况越背离。而对于这个联合概率,我们可以通过计算参数的最大似然估计的那一套方法来确定使得联合概率最大的参数$W$,此时的W就是我们要选的最佳参数,它使得联合概率最大(即代价函数最小)。下面看具体的运算步骤。
关于参数的最大似然估计的相关知识可以参考博客: [最大化期望算法(EM)详解](https://blog.csdn.net/guoziqing506/article/details/81274276)
# 逻辑回归的运算步骤
## 写出最大似然函数,并进行对数化处理
::: hljs-center
$\begin{aligned} L(W) &=\sum_{i=1}^{n} \ln p\left(y_{i} \mid X_{i} ; W\right) \\ &=\sum_{i=1}^{n} \ln \left(\phi\left(z_{i}\right)^{y_{i}}\left(1-\phi\left(z_{i}\right)\right)^{1-y_{i}}\right) \\ &=\sum_{i=1}^{n} y_{i} \ln \phi\left(z_{i}\right)+\left(1-y_{i}\right) \ln \left(1-\phi\left(z_{i}\right)\right.\end{aligned}$
:::
通过上面的分析,显然 −$L(W)$ 就是代价函数$J(W)$。为方便后面的推导,我把$J(W)$也写出来:
::: hljs-center
$J(W)=-\sum_{i=1}^{n} y_{i} \ln \phi\left(z_{i}\right)+\left(1-y_{i}\right) \ln \left(1-\phi\left(z_{i}\right)\right)$
:::
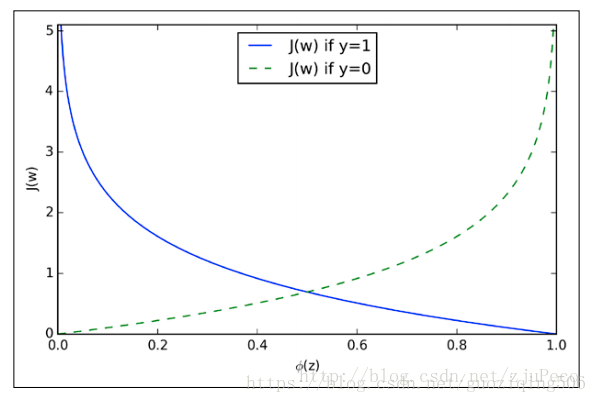
$J(W)$ 的图像如下所示:
::: hljs-center
:::
可以看出,如果类标号为1,那么$ϕ(z)$的取值在$[0,1]$范围内增大时,代价函数减小,说明越接近真实情况,代价就越小;如果类标号为0,也是一样的道理。
## 用梯度下降法求代价函数的最小值
如果能求出代价函数的最小值,也就是最大似然函数的最大值。那么得到的权重向量$W$就是逻辑回归的最终解。但是通过上面的图像,你也能发现,$J(W)$是一种非线性的$S$型函数,不能直接利用偏导数为0求解。于是我们采用梯度下降法。
首先,根据梯度的相关理论,我们知道梯度的负方向就是代价函数下降最快的方向。因此,我们应该沿着梯度负方向逐渐调整权重分量$w_j$,直到得到最小值,所以每个权重分量的变化应该是这样的:
::: hljs-center
$\Delta w_{j}=-\eta \frac{\partial J(W)}{\partial w_{j}}$
:::
其中$η$为学习率,控制步长。而 $\frac{\partial J(W)}{\partial w_{j}}$ 可以如下计算:
::: hljs-center
$\begin{aligned} \frac{\partial J(w)}{\partial w_{j}} &=-\sum_{i=1}^{n}\left(y_{i} \frac{1}{\phi\left(z_{i}\right)}-\left(1-y_{i}\right) \frac{1}{1-\phi\left(z_{i}\right)}\right) \cdot \frac{\partial \phi\left(z_{i}\right)}{\partial w_{j}} \\ &=-\sum_{i=1}^{n}\left(y_{i}\left(1-\phi\left(z_{i}\right)\right)-\left(1-y_{i}\right) \phi\left(z_{i}\right)\right) \cdot x_{i j} \\ &=-\sum_{i=1}^{n}\left(y_{i}-\phi\left(z_{i}\right)\right) \cdot x_{i j} \end{aligned}$
:::
上式的推导中用到了$Sigmoid$函数$ϕ(z)$的一个特殊的性质:
::: hljs-center
$\phi(z)^{\prime}=\phi(z)(1-\phi(z))$
:::
这样,我们就得到了梯度下降法更新权重的变量:
::: hljs-center
$w_{j+1}:=w_{j}+\eta \sum_{i=1}^{n}\left(y_{i}-\phi\left(z_{i}\right)\right) \cdot x_{i j}$
:::
最后,说一下权重向量的初始化问题。一般用接近于0的随机值初始化$w_j$,比如在区间 $[−0.01,0.01]$ 内均匀选取。这样做的理由是如果$w_i$很大,则加权和可能也很大,根据$Sigmoid$函数的图像(即本文的第一个图像)可知,大的加权和会使得$ϕ(z_i)$的导数接近0,则变化速率变缓使得权重的更新变缓。
---
转载:[逻辑回归(logistic regression)原理详解](https://blog.csdn.net/guoziqing506/article/details/81328402)