决策树-回归
**核心:划分点选择 + 输出值确定**
## 1 概述
决策树是一种基本的分类与回归方法,本文叙述的是回归部分。回归决策树主要指CART(classification and regression tree)算法,内部结点特征的取值为“是”和“否”, 为二叉树结构。
所谓回归,就是根据特征向量来决定对应的输出值。回归树就是将特征空间划分成若干单元,每一个划分单元有一个特定的输出。因为每个结点都是“是”和“否”的判断,所以划分的边界是平行于坐标轴的。对于测试数据,我们只要按照特征将其归到某个单元,便得到对应的输出值。
>【例】左边为对二维平面划分的决策树,右边为对应的划分示意图,其中c1,c2,c3,c4,c5是对应每个划分单元的输出。
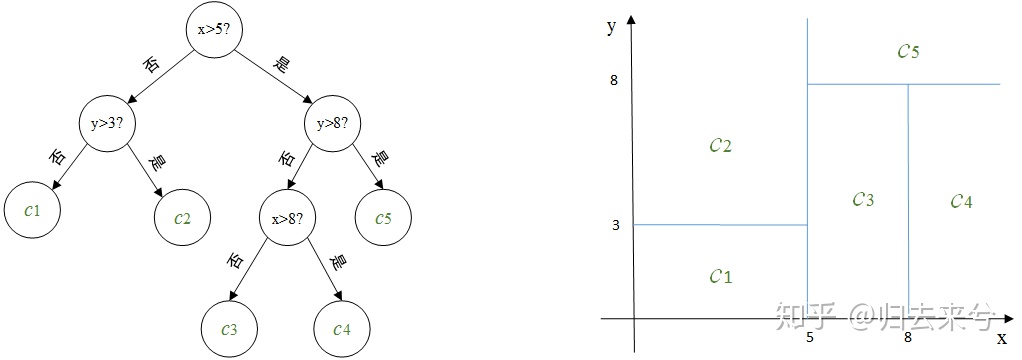
>如现在对一个新的向量(6,6)决定它对应的输出。第一维分量6介于5和8之间,第二维分量6小于8,根据此决策树很容易判断(6,6)所在的划分单元,其对应的输出值为c3。
划分的过程也就是建立树的过程,每划分一次,随即确定划分单元对应的输出,也就多了一个结点。当根据停止条件划分终止的时候,最终每个单元的输出也就确定了,也就是叶结点。
## 2 回归树建立
既然要划分,切分点怎么找?输出值又怎么确定?这两个问题也就是回归决策树的核心。
**[切分点选择:最小二乘法] ;[输出值:单元内目标值的均值]**
### 2.1 原理
假设X和Y分别为输入和输出变量,并且Y是连续变量,给定训练数据集为
$D=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{N}, y_{N}\right)\right\},$ 其中 $x_{i}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \ldots, x_{i}^{(n)}\right)$为输入实例(特征向量),n为特征个数,i=1,2,...,N, N为样本容量。
**对特征空间的划分采用启发式方法,每次划分逐一考察当前集合中所有特征的所有取值,根据平方误差最小化准则选择其中最优的一个作为切分点。** 如对训练集中第j个特征变量 $x^{(j)}$ 和它的取值$s$,作为切分变量和切分点,并定义两个区域$R_{1}(j, s)=\left\{x \mid x^{(j)} \leqslant s\right\}$和$R_{2}(j, s)=\left\{x \mid x^{(j)}>s\right\}$为找出最优的 $j$ 和 $s$ ,对下式求解
::: hljs-center
$\min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right]$ (1.1)
:::
也就是找出使要划分的两个区域平方误差和最小的 $j$ 和 $s$ 。
其中, $c_1$ , $c_2$ 为划分后两个区域内固定的输出值,方括号内的两个min意为使用的是最优的 $c_1$ 和 $c_2$ ,也就是使各自区域内平方误差最小的$c_1$和 $c_2$ ,**易知这两个最优的输出值就是各自对应区域内Y的均值**,所以上式可写为
::: hljs-center
$\min _{j, s}\left[\sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-\hat{c}_{1}\right)^{2}+\sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-\hat{c_{2}}\right)^{2}\right]$ (1.2)
其中 $\hat{c_{1}}=\frac{1}{N_{1}} \sum_{x_{i} \in R_{1}(j, s)} y_{i}, \quad \hat{c_{2}}=\frac{1}{N_{2}} \sum_{x_{i} \in R_{2}(j, s)} y_{i}$
:::
现证明一维空间中样本均值是最优的输出值(平方误差最小):
>给定一个随机数列 $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ ,设该空间中最优的输出值为 $a$ ,根据最小平方误差准则,构造 $a$ 的函数如下:
::: hljs-center
$F(a)=\left(x_{1}-a\right)^{2}+\left(x_{2}-a\right)^{2}+\ldots+\left(x_{n}-a\right)^{2}$
:::
考察其单调性,
::: hljs-center
$F^{\prime}(a)=-2\left(x_{1}-a\right)-2\left(x_{2}-a\right)+\ldots-2\left(x_{n}-a\right)=2 n a-2 \sum_{i=1}^{n} x_{i}$
:::
令 $F^{\prime}(a)=0$ ,得 $a=\frac{1}{n} \sum_{i=1}^{n} x_{i}$
根据其单调性,易知 $\hat{a}=\frac{1}{n} \sum_{i=1}^{n} x_{i}$ 为最小值点。证毕。
找到最优的切分点 $(j,s)$后,依次将输入空间划分为两个区域,接着对每个区域重复上述划分过程,直到满足停止条件为止。这样就生成了一棵回归树,这样的回归树通常称为**最小二乘回归树**。
### 2.2 树分裂的停止条件
有了选取分割特征和最佳分割点的方法,树便可以依此进行分裂,但是分裂的终止条件是什么呢?
- **结点中所有目标变量的值相同**, 既然都已经是相同的值了自然没有必要在分裂了,直接返回这个值就好了.
- **树的深度达到了预先指定的最大值**
- **不纯度的减小量小于预先定好的阈值**,也就是之进一步的分割数据并不能更好的降低数据的不纯度的时候就可以停止树分裂了。
- **结点的数据量小于预先定好的阈值**
### 2.3 算法叙述
输入:训练数据集D;
输出:回归树f(x).
在训练数据集所在的输入空间中,递归地将每个区域划分为两个子区域并决定每个子区域上的输出值,构建二叉决策树:
1) 选择最优切分变量j与切分点s,求解
$\min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right]$ (1.3)
遍历变量 $j$ ,对固定的切分变量 $j$ 扫描切分点 $s$ ,选择使上式达到最小值的对 $(j,s)$ 。
2) 用选定的对 $(j,s)$ 划分区域并决定相应的输出值:
$\hat{c_{m}}=\frac{1}{N_{m}} \sum_{x_{i} \in R_{m}(j, s)} y_{i}, \quad x \in R_{m}, m=1,2$ (1.4)
其中, $\quad R_{1}(j, s)=\left\{x \mid x^{(j)} \leqslant s\right\}, \quad R_{2}(j, s)=\left\{x \mid x^{(j)}>s\right\}$
3) 继续对两个子区域调用步骤(1),(2),直至满足停止条件。
4) 将输入空间划分为M个区域 $R_{1}, R_{2}, \ldots, R_{M}$ ,生成决策树:
$f(x)=\sum_{m=1}^{M} c_{m} I\left(x \in R_{m}\right)$
其中 $I$ 为指示函数, $\quad I=\left\{\begin{array}{ll}1 & i f\left(x \in R_{m}\right) \\ 0 & i f\left(x \notin R_{m}\right)\end{array}\right.$
## 3 示例
下表为训练数据集,特征向量只有一维,根据此数据表建立回归决策树。

**(1) 选择最优切分变量j与最优切分点s:**
在本数据集中,只有一个特征变量,最优切分变量自然是x。接下来考虑9个切分点 \{1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5\} (切分变量两个相邻取值区间 $\left[a^{i}, a^{i+1}\right)$ 内任一点均可),根据式(1.2)计算每个待切分点的损失函数值:
损失函数为(同式(1.2))
::: hljs-center
$L(j, s)=\sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-\hat{c_{1}}\right)^{2}+\sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-\hat{c_{2}}\right)^{2}$
其中 $\hat{c_{1}}=\frac{1}{N_{1}} \sum_{x_{i} \in R_{1}(j, s)} y_{i}, \quad \hat{c_{2}}=\frac{1}{N_{2}} \sum_{x_{i} \in R_{2}(j, s)} y_{i}$
:::
a. 计算子区域输出值
当s=1.5时,两个子区域 $R_{1}=\{1\}, \quad R_{2}=\{2,3,4,5,6,7,8,9,10\}$ $c_{1}=5.56$ $c_{2}=\frac{1}{9}(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)=7.5$
同理,得到其他各切分点的子区域输出值,列表如下

b. 计算损失函数值,找到最优切分点
当s=1.5时,$L(1.5)=(5.56-5.56)^{2}+\left[(5.7-7.5)^{2}+(5.91-7.5)^{2}+\ldots+(9.05-7.5)^{2}\right]=0+15.72=15.72$
同理,计算得到其他各切分点的损失函数值,列表如下

易知,取s=6.5时,损失函数值最小。因此,第一个划分点为(j=x,s=6.5).
**(2) 用选定的对 $(j,s)$ 划分区域并决定相应的输出值:**
划分区域为: $R_{1}=\{1,2,3,4,5,6\}, \quad R_{2}=\{7,8,9,10\}$
对应输出值: $c_{1}=6.24, \quad c_{2}=8.91$
**(3) 调用步骤(1),(2),继续划分:**
对 $R_1$ ,取切分点 $\{1.5,2.5,3.5,4.5,5.5\}$ ,计算得到单元输出值为
::: hljs-center

:::
损失函数值为
::: hljs-center

:::
L(3.5)最小,取s=3.5为划分点。
后面同理。
**(4) 生成回归树:**
假设两次划分后即停止,则最终生成的回归树为:
::: hljs-center

:::
## 4 Python实现
对第三部分例子的python实现及与线性回归对比。
```PYTHON
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn import linear_model
# Data set
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05]).ravel()
# Fit regression model
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=3)
model3 = linear_model.LinearRegression()
model1.fit(x, y)
model2.fit(x, y)
model3.fit(x, y)
# Predict
X_test = np.arange(0.0, 10.0, 0.01)[:, np.newaxis]
y_1 = model1.predict(X_test)
y_2 = model2.predict(X_test)
y_3 = model3.predict(X_test)
# Plot the results
plt.figure()
plt.scatter(x, y, s=20, edgecolor="black",
c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue",
label="max_depth=1", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=3", linewidth=2)
plt.plot(X_test, y_3, color='red', label='liner regression', linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
```
运行结果为
::: hljs-center
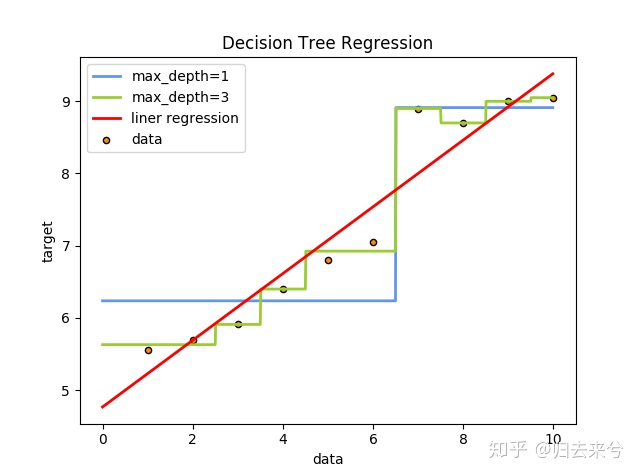
:::

> 基尼指数中讲述的例子,正是使用了one-hot之后的结果
---
转载:[决策树—回归](https://zhuanlan.zhihu.com/p/42505644)