LASSO回归
在线性回归模型中,其参数估计公式为$\beta=\left(X^{T} X\right)^{-1} X^{T} y$,当$X^TX$ 不可逆时无法求出$β$,另外如果$|X^TX|$ 越趋近于0,会使得回归系数趋向于无穷大,此时得到的回归系数是无意义的。解决这类问题可以使用岭回归和LASSO回归,主要针对**自变量之间存在多重共线性**或者**自变量个数多于样本量**的情况。
**[线性模型-多重共线性问题的解决-Lasso](https://blog.csdn.net/gracejpw/article/details/102495464)**
## 1 参数推导
岭回归无法剔除变量,而LASSO回归模型,将惩罚项由L2范数变为L1范数,可以将一些不重要的回归系数缩减为0,达到剔除变量的目的。
$\begin{aligned} J(\beta) &=\sum(y-X \beta)^{2}+\lambda\|\beta\|_{1} =\sum(y-X \beta)^{2}+\sum \lambda \mid \beta =E S S(\beta)+\lambda l_{1}(\beta) \end{aligned}$
其中$ESS(β)$=表示误差平方和,$\lambda l_{1}(β)$ 表示惩罚项。由于惩罚项变成了绝对值,则在零点处就不可导,故采用坐标下降法(对于p维参数的可微凸函数$J(β)$,如果存在$\hat{\beta}$使得$J(β)$在每个坐标轴上均达到最小值,则$J \hat{(\beta)}$就是点$\hat{\beta}$上的全局最小值),控制其他p-1个参数不变,对目标函数中的某一个$β_j$求偏导,以此类推对剩下的p-1个参数求偏导,最终令每个分量下的导函数为0,得到使目标函数达到全局最小的$\hat{\beta}$
$\begin{aligned} & E S S(\beta)=\sum_{i=1}^{n}\left(y_{i}-\sum_{j=1}^{p} \beta x_{i j}\right)^{2} = \sum_{i=1}^{n}\left(y_{i}^{2}+\left(\sum_{j=1}^{p} \beta_{j} x_{i j}\right)^{2}-2 y_{i}\left(\sum_{j=1}^{p} \beta_{j} x_{i j}\right)\right) \end{aligned}$
$\Rightarrow \frac{\partial E S S(\beta)}{\partial \beta_{j}}=-2 \sum_{i=1}^{n} x_{i j}\left(y_{i}-\sum_{j=1}^{p} \beta_{j} x_{i j}\right)$
$=-2 \sum_{i-1}^{n} x_{i j}\left(y_{i}-\sum_{k=j} \beta_{k} x_{i k}-\beta_{j} x_{i j}\right)$
$=-2 \sum_{i=1}^{n} x_{i j}\left(y_{i}-\sum_{k=j} \beta_{k} x_{i k}\right)+2 \beta_{j} \sum_{i=1}^{n} x_{i j}^{2}$
$=-2 m_{j}+2 \beta_{j} n_{j}$
其中 $m_{j}=\sum_{i-1}^{n} x_{i j}\left(y_{i}-\sum_{k=j} \beta_{k} x_{i k}\right), \quad n_{j}=\sum_{i=1}^{n} x_{i j}^{2}$
惩罚项不可导,则使用次导数:
$\frac{\partial \lambda_{l}(\beta)}{\partial \beta_{j}}=\left\{\begin{array}{ll}\lambda, & \text { 当 } \beta_{j}>0 \\ {[-\lambda, \lambda],} & \text { 当 } \beta_{j}=0 \\ -\lambda, & \text { 当 } \beta_{j}<0\end{array}\right.$
于是令两个偏导数相加等于0
$\frac{\partial E S S(\beta)}{\partial \beta_{j}}+\frac{\partial \lambda l_{1}(\beta)}{\partial \beta_{j}}=\left\{\begin{array}{l}-2 m_{j}+2 \beta_{j} n_{j}+\lambda=0 \\ {\left[-2 m_{j}-\lambda,-2 m_{j}+\lambda\right]=0} \\ -2 m_{j}+2 \beta_{j} n_{j}-\lambda=0\end{array}\right.$
$\Rightarrow \beta_{j}=\left\{\begin{array}{ll}\left(m_{j}-\frac{\lambda}{2}\right) / n_{j}, & \text { 当 } m_{j}>\frac{\lambda}{2} \\ 0, & \text { 当 } m_{j} \in\left[-\frac{\lambda}{2}, \frac{\lambda}{2}\right] \\ \left(m_{j}+\frac{\lambda}{2}\right) / n_{j}, & \text { 当 } m_{j}<\frac{\lambda}{2}\end{array}\right.$

## 2 $λ$的选择
直接使用交叉验证法
>LassoCV(eps=0.001, n_alphas=100, alphas=None, fit_intercept=True, normalize=False, precompute=‘auto’, max_iter=1000, tol=0.0001, copy_X=True, cv=None, verbose=False, n_jobs=1, positive=False, random_state=None, selection=‘cyclic’)
• eps:指代λλ最小值与最大值的商,默认为0.001。
• n_alphas:指定λλ的个数,默认为100个。
• alphas:指定具体的λλ列表用于模型的运算。
• fit_intercept:bool类型,是否需要拟合截距项,默认为True。
• normalize:bool类型,建模时是否对数据集做标准化处理,默认为False。
• precompute:bool类型,是否在建模前计算Gram矩阵提升运算速度,默认为False。
• max_iter:指定模型的最大迭代次数。
• tol:指定模型收敛的阈值,默认为0.0001。
• copy_X:bool类型,是否复制自变量X的数值,默认为True。
• cv:指定交叉验证的重数。
• verbose:bool类型,是否返回模型运行的详细信息,默认为False。
• n_jobs:指定使用的CPU数量,默认为1,如果为-1表示所有CPU用于交叉验证的运算。
• positive:bool类型,是否将回归系数强制为正数,默认为False。
• random_state:指定随机生成器的种子。
• selection:指定每次迭代选择的回归系数,如果为’random’,表示每次迭代中将随机更新回归系数;如果为’cyclic’,则每次迭代时回归系数的更新都基于上一次运算。
```python
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import LassoCV
data=pd.read_excel(r'C:\Users\Administrator\Desktop\diabetes.xlsx')
#拆分为训练集和测试集
predictors=data.columns[:-1]
x_train,x_test,y_train,y_test=model_selection.train_test_split(data[predictors],data.Y,
test_size=0.2,random_state=1234)
#构造不同的lambda值
Lambdas=np.logspace(-5,2,200)
#设置交叉验证的参数,使用均方误差评估
lasso_cv=LassoCV(alphas=Lambdas,normalize=True,cv=10,max_iter=10000)
lasso_cv.fit(x_train,y_train)
print(lasso_cv.alpha_)
```

## 3 代码实现
>Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection=‘cyclic’)
• alphas:指定λλ值,默认为1。
• fit_intercept:bool类型,是否需要拟合截距项,默认为True。
• normalize:bool类型,建模时是否对数据集做标准化处理,默认为False。
• precompute:bool类型,是否在建模前计算Gram矩阵提升运算速度,默认为False。
• copy_X:bool类型,是否复制自变量X的数值,默认为True。
• max_iter:指定模型的最大迭代次数。
• tol:指定模型收敛的阈值,默认为0.0001。
• warm_start:bool类型,是否将前一次训练结果用作后一次的训练,默认为False。
• positive:bool类型,是否将回归系数强制为正数,默认为False。
• random_state:指定随机生成器的种子。
• selection:指定每次迭代选择的回归系数,如果为’random’,表示每次迭代中将随机更新回归系数;如果为’cyclic’,则每次迭代时回归系数的更新都基于上一次运算。
```python
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import Lasso,LassoCV
from sklearn.metrics import mean_squared_error
data=pd.read_excel(r'C:\Users\Administrator\Desktop\diabetes.xlsx')
data=data.drop(['AGE','SEX'],axis=1)
#拆分为训练集和测试集
predictors=data.columns[:-1]
x_train,x_test,y_train,y_test=model_selection.train_test_split(data[predictors],data.Y,
test_size=0.2,random_state=1234)
#构造不同的lambda值
Lambdas=np.logspace(-5,2,200)
#设置交叉验证的参数,使用均方误差评估
lasso_cv=LassoCV(alphas=Lambdas,normalize=True,cv=10,max_iter=10000)
lasso_cv.fit(x_train,y_train)
#基于最佳lambda值建模
lasso=Lasso(alpha=lasso_cv.alpha_,normalize=True,max_iter=10000)
lasso.fit(x_train,y_train)
#打印回归系数
print(pd.Series(index=['Intercept']+x_train.columns.tolist(),
data=[lasso.intercept_]+lasso.coef_.tolist()))
#模型评估
lasso_pred=lasso.predict(x_test)
#均方误差
MSE=mean_squared_error(y_test,lasso_pred)
print(MSE)
```
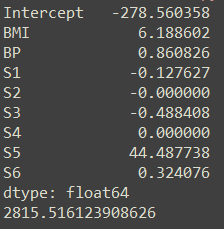
相对于岭回归而言,可以看到LASSO回归剔除了两个变量,降低了模型的复杂度,同时减少了均方误差,提高了模型的拟合效果。
---
转载:[机器学习十大经典算法之岭回归和LASSO回归(学习笔记整理)](https://blog.csdn.net/weixin_43374551/article/details/83688913)